
작성자: 김정한 이사 ㅣDB R&D센터 l Tech Biz. 팀
개요
본 아티클에서는 벡터 데이터베이스를 논의하며, 기본 개념을 넘어 벡터의 주요 연산부터 시작합니다. 특히, 벡터 데이터베이스는 쿼리를 통해 가장 유사한 결과를 비교하고 식별하는 기반이 되는 벡터 유사도를 다룹니다. 필요한 경우에만 수학적 표현과 기하적 표현을 사용하며, 실제 파이썬 코딩 예시를 함께 제공할 예정입니다.
다음 연재에 벡터 임베딩(데이터의 특정 Feature를 포착하는 데이터의 수치적 표현)과 인덱싱 알고리즘, Semantic Search(기본적으로 텍스트의 의미나 이미지에 포함된 개체 등 유사성을 기준으로 검색하는 것)에 대하여 알아보도록 하겠습니다. 이어서 벡터 Indexing 기법들을 알아보고 OSS(Open Source Software) 벡터 데이터베이스들과 PostgreSQL pgvector의 장단점 소개 및 비교 테스트, 마지막으로 벡터 데이터베이스(pgvector)의 LLM과 RAG 응용에 대한 부분을 차례로 다룰 예정입니다.
Vector 연산
벡터 데이터베이스에 저장되는 벡터는 선형대수(Linear Algebra)에서 데이터의 개수나 형태에 따라 크게 스칼라(scalar), 벡터(vector), 행렬(matrix), 텐서(tensor)로 나뉘는 유형중 하나로 스칼라는 숫자 하나로 이루어진 데이터입니다. 벡터는 여러 숫자로 이루어진 데이터 레코드(data record로 array와 같은)이며, 행렬은 이러한 벡터, 데이터 레코드가 여러개인 데이터 집합이라고 볼 수 있습니다. 텐서는 같은 크기의 행렬이 여러 개 있는 것이라고 생각하면 되겠습니다.
Vector 내적/외적
그럼 먼저 벡터의 연산에 대하여 주요한 몇 가지를 알아보도록 하겠습니다. 벡터를 가지고 연산하는 방법은 여러 가지가 있지만 데이터 분석, ML/DL 및 AI와 관련되어서는 벡터의 각 성분을 곱한 후 그 결과를 모두 더하는 내적(Dot Product)과 두 벡터의 성분을 활용하여 새로운 벡터를 생성하는 외적(Cross Product)이 주된 연산법이 있습니다. 파이썬을 사용하여 임의의 두 벡터(array)를 계산해보겠습니다.
* Dot Product는 Inner Product 라고 표현되기도 함.
<Python Vector 연산> * Numpy : 다차원 배열을 쉽게 처리하고 효율적으로 사용할 수 있도록 지원하는 파이썬의 패키지
| import numpy as np #Numpy Library # 3차원 벡터 생성 v1 = np.array([5, 6, 1]) v2 = np.array([6, -1, 2]) # 벡터내적 dot Product dot_product = np.dot(v1, v2) print("dotprod.:", dot_product) # 벡터외적 cross Product cross_product = np.cross(v1, v2) print("crossprod.:", cross_product) |
결과
| dotprod.: 26 crossprod.: [13 -4 -41] |
이러한 벡터의 내적(Dot Product)연산은 데이터 분석에서 사용되는 가중합(weighted sum)에서 사용됩니다. 예를 들어 만약 데이터 벡터가 𝑥=[𝑥1,⋯,𝑥𝑁]𝑇 이고 가중치 벡터가 𝑤=[𝑤1,⋯,𝑤𝑁]𝑇 이면 데이터 벡터의 가중합을 수식으로 표현하면 다음과 같습니다:
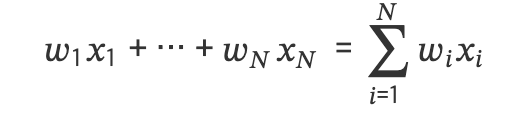
다음으로는 가중평균(weighted average)에 대해 알아보겠습니다. 벡터로 표현된 𝑁개의 데이터의 단순 평균은 아래와 같은 수식으로 나타낼 수 있습니다:

이러한 내적연산은 정규화/비정규화 데이터셋에 모두 적합합니다. 추후에 다룰 인덱싱을 위한 유사도(similarity) 측정에도 사용됩니다.
유사도
유사도란 두 벡터가 닮은 정도를 정량적으로 나타낸 값입니다. 두 벡터가 비슷한 경우에는 유사도가 크고 비슷하지 않은 경우에는 유사도가 작아집니다. 유사도 측정에는 내적(Dot Product)이외에도
- 코사인 유사도(cosine similarity)
- 유클리드 거리(Euclidean Distance) or L2 Distance
- 맨해튼 거리(Manhattan Distance) or L1 Distance
- 해밍 거리(Hamming Distance)
- 자카드 거리(Jaccard Distance)
- 피어슨 유사도(Pearson Similarity)
등이 있으며, 벡터 데이터베이스에서 사용자의 쿼리를 받으면 인덱스 벡터를 쿼리 벡터와 비교하여 가장 가까운(유사한) 벡터를 결정하기 위하여 위와 같은 유사도 측정법들이 사용됩니다. 개념적으로 이해하는것이 중요합니다. 아래 이미지는 앞으로 다룰 오픈소스 데이터베이스 PostgreSQL의 벡터 익스텐션인 pgvector의 Github에 주요 기능 중 지원되는 유사도 측정법을 보여줍니다. 위에 나열한 측정법들과 매칭되는 것들도 보입니다.
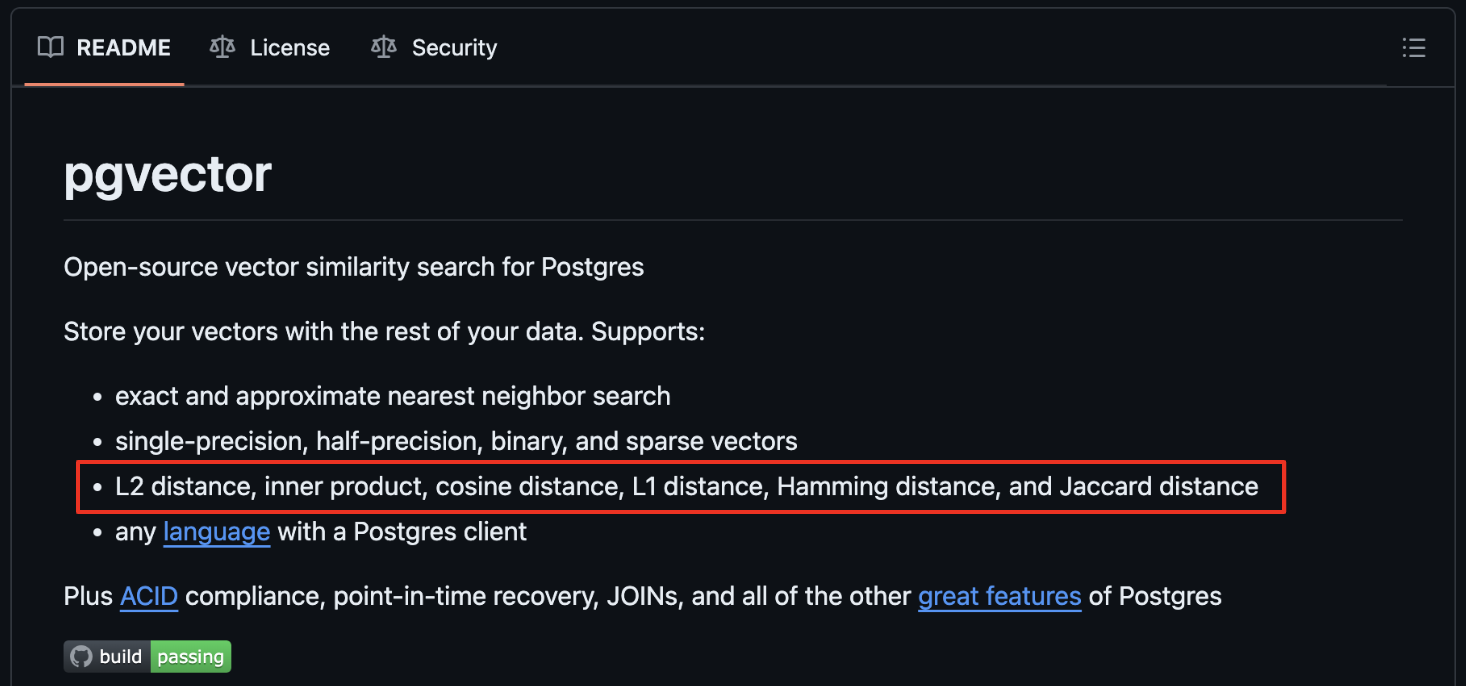
pgvector에서는 용어를 L1 과 L2를 사용하였는데, Manhattan distance와 Euclidean distance와 같은 의미이며, Manhattan distance는 두 점의 좌표 차이의 절대값의 합이고, Euclidean distance는 두 점 사이의 직선 거리를 말합니다.
그럼, 대표적인 유사도 몇 가지를 알아보도록 하겠습니다. 우리가 직관적으로 생각하는 두 지점간의 직선 거리라는 개념과 유사한 유클리드 거리(Euclidean Distance)부터 알아보도록 하겠습니다.
유클리드 거리(Euclidean Distance)
두 점인 a, b간의 벡터인 Norm의 정의와 벡터의 차의 정의에서 유클리드 거리는 다음과 같은 식을 구할 수 있습니다.
* Norm : 놈(norm)은 쉽게 말해 두 점 사이의 거리를 일반화한 개념으로 ||a|| 로 표현함.(이 외에도 여러가지 Norm이 있음)
* aT : 벡터의 전치(Transpose) 연산을 위하여 열과 행을 바꾸는것.
.
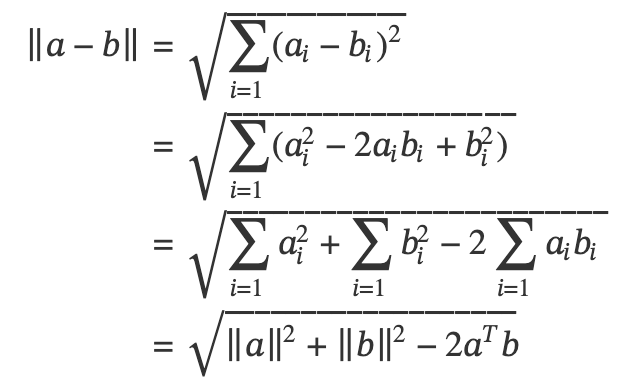

복잡한 수학식보다는 파이썬 numpy에 선형대수모듈 linalg.norm() 함수로 임의의 두 벡터(array)간 거리를 간단히 계산해보겠습니다.
<Python 유클리드 거리>
| # using linalg.norm() import numpy as np # numpy arrays point1 = np.array((2, -1, 3)) point2 = np.array((1, 2, 1)) # linalg.norm()을 사용하여 유클리드거리 계산 dist = np.linalg.norm(point1 - point2) # printing Euclidean distance print(dist) |
결과
| 3.7416573867739413 |
다음은 많이 사용되는 코사인 유사도(cosine similarity)를 설명합니다.
코사인 유사도(cosine similarity)
벡터는 크기와 방향을 가지는데, 두 벡터의 방향이 유사할수록 그들이 비슷하다고 간주하며, 이를 측정하기 위해 두 벡터 사이의 각의 코사인값을 사용합니다.
유클리드 거리와 마찬가지로 두 벡터 x,y간의 코사인 유사도를 수학식으로 표현해보면 다음과 같습니다.
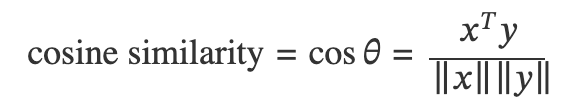
여기서 Norm ||x||와 ||y||는 위의 유클리드 거리에서도 논한바와 같이 벡터 x와 y의 크기(길이)입니다. 코사인 유사도의 범위는 -1에서 1까지이며, 1은 동일한 방향(0°), 0은 직교(90°), 그리고 -1은 반대 방향(180°)을 나타냅니다.

여기서 재미있는 점은 단어를 가지고 feature 벡터화 하여 코사인 유사도를 측정할 때는 음수가 나올수 없어 90도일때가 가장 단어간의 관계성이 없습니다. 예를 들어 “happy” 라는 단어를 예로 들자면 비슷한 의미의 “love”같은 단어는 코사인 유사도 1에 가까운 값이 나오고 “monitor” 같은 단어는 관계성이 없으므로 0에 가까운 값이 나온다는 것입니다. 이처럼 코사인 유사도는 자연어처리(NLP)의 텍스트 분석, 추천 시스템, K-Means 클러스터링 알고리즘에도 사용되며 pgvector에서도 사용되는 범용적인 유사도입니다.
뒤에서 임베딩을 다루기 전이지만, 자연어처리(NLP) 모델 Word2Vec에서, 예시로 “Queen”과 “King” 두 단어를 벡터화하면 다음과 같이 수치적으로 표현될 것입니다. 이 벡터들은 2차원 평면에서 아래에 나열된 수치와 같이 유사도가 높고(방향이 유사하게) 표현됩니다.
| Queen = [1.5, -0.4, 7.2, 19.6, 3.1, ..., 20.2] King = [1.5, -0.4, 7.2, 19.5, 3.2, ..., 20.8] |
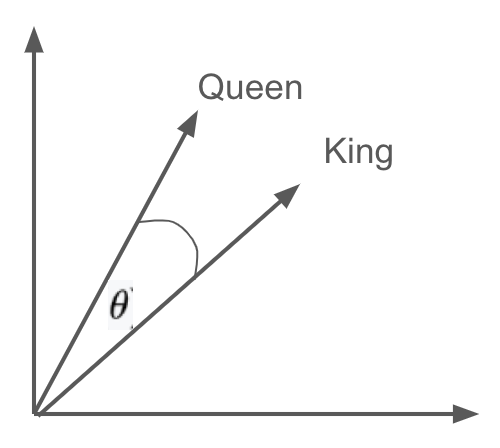
이를 통해 벡터 기반 표현은 수치적 연산이 가능해지며, 센세이션을 일으킨 아래 예제와 같이 단어간 연산이 가능해집니다.
| "king − man + woman ≈ queen" |
"King"과 "man"의 차이(feature vector)가 "왕족"이라는 것을 나타내며, 이는 "queen"에서 "woman"을 뺀 것이라는 것을 수학적으로 유추할 수 있습니다.
파이썬 코드를 통해 보겠습니다. 앞에 사용한 것과 같이 Python Numpy 의 Norm과 내적(Dot Product)으로 계산할 수도 있지만, 파이썬 M/L Open-source Library Scikit-Learn 1.5 에서 “cosine_similarity( )”함수를 제공하고 있으므로 이를 간편하게 사용해 보겠습니다.
<Python 코사인 유사도>
| # using Scikit-learn(sklearn) cosine_similarity() from sklearn.metrics.pairwise import cosine_similarity Queen = [[1.5, -0.4, 7.2, 19.6, 3.1, 20.2]] King = [[1.5, -0.4, 7.2, 19.5, 3.2, 20.8]] # printing cosine_similarity print(cosine_similarity(Queen, King)) |
결과
| [[0.99985641]] |
스케일변화의 측면에서는 유클리드 거리는 데이터간에 스케일변화가 크지 않을때, 코사인은 스케일차이가 클때 주로 활용된다고 볼 수 있다.
해밍 거리(Hamming Distance)
해밍 거리(Hamming Distance)는 위키백과에 정의를 보면 “블록 부호 이론에서, 해밍 거리(Hamming距離, 영어: Hamming distance)는 곱집합 위에 정의되는 거리 함수이다”라고 되어 있고 “대략, 같은 길이의 두 문자열에서, 같은 위치에서 서로 다른 기호들이 몇 개인지를 센다.” 설명만으로는 조금 복잡하기 때문에 예제를 통한 간단히 계산법을 보면서 개념적인 설명을 하겠습니다.
예제)
'1011101'과 '1001001'사이의 해밍 거리는 2이다. (1011101, 1001001)
'2143896'과 '2233796'사이의 해밍 거리는 3이다. (2143896, 2233796)
"toned"와 "roses"사이의 해밍 거리는 3이다. (toned, roses)
첫번째 예제에서 보이듯 두 집합(2진벡터)내의 XOR 연산을 통한 합산 값이 거리가 되는것을 볼 수 있습니다.

대부분의 벡터는 부동 소수점(Float)으로 표현되다 보니 해밍 거리는 두 텍스트 간의 어법의 차이, 단어의 철자의 차이 또는 임의의 두 이진 벡터 간의 차이와 같은 것을 측정하거나 sparse 벡터간의 차이를 측정하는 데 좋습니다.
* sparse 벡터 : 밀집 벡터와 대비되는 개념으로 ‘희소 벡터(sparse vector)’가 있다. 희소 벡터는 분석 대상인 모든 단어가 가진 모든 속성을 차원으로 설정하여, 대부분의 요소 값이 0인 벡터를 의미한다.
해밍거리는 NLP에 TF-IDF(Term Frequency-Inverse Document Frequency), 협업 필터링(collaborative filtering) 등 추천시스템 데이터 분석에도 사용되고 있습니다.
자카드 거리(Jaccard Distance)
자카드 거리(Jaccard Distance)는 Jaccard coefficient라고도 하며 먼저 자카드 유사도를 계산하고 1에서 자카드 유사도 값을 뺀 값으로 측정됩니다. 두 집합 A, B에 대하여 아래와 같은 수식으로 표현됩니다만, 그림과 함께 아주 간단한 계산으로 쉽게 설명 하겠습니다.

아래 그림과 같이 두 집합간에 합집합 = 12, 교집합 = 3 일경우, 자카드 유사도 = 3/12 (0.25), 즉 자카드 거리는 1-0.25 = 0.75 입니다.

당연한 얘기이지만 두 집합 사이의 교집합이 클수록 유사도가 높습니다.
여기까지 pgvector에서 지원되는 주요유사도에 대하여 이해를 가져 보았습니다.
벡터 데이터베이스는 이미지, 텍스트, 오디오, 센서 데이터와 같은 비정형 / 반정형 데이터를 데이터 객체의 속성에 따라 고차원 벡터 공간에 임베딩하고, 각 벡터 간의 관계를 정의하며 특정 알고리즘(Hashing, Quantization, Graph 등)에 따라 인덱싱하는 방식입니다. 이 과정에서 유사도 측정은 주어진 쿼리에 대해 벡터 데이터베이스가 가장 관련성이 높은(유사한) 결과를 비교하고 식별하는 기초가 됩니다. 따라서 유사도에 대한 이해는 반드시 필요합니다. 본 기고문에서 다루지 않은 유사도나 더 깊은 영역에 관심이 있는 독자들에게는 추가적으로 파헤쳐 보시기를 권장드립니다.
이어서 다음 연재에는 벡터 임베딩에 관해 알아보며 KNN, ANN 검색 알고리즘, 관계형 DBMS의 B-Tree 와 같은 벡터 Indexing으로 Hashing, Product Quantization, Graph 기반한 기법들에 대해 알아보도록 하겠습니다.
